Modellmethode

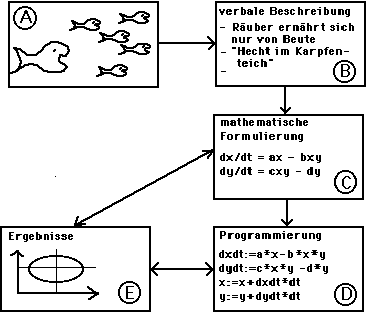
Abb. 1: Stufen des Modellbildungsprozesses und der computerunterstützten Modellbildung (Erläuterungen im Text).

Wir gehen aus von einem mentalen Modell der Lernenden über das Phänomen, basierend auf ihren Vorkenntnissen, auf Alltagswissen bzw. auf dem im Unterricht bereits vermittelten Fachwissen (Abb. 1A). Dieses mentale Modell kann verbalisiert werden. Es ist möglich, eine Beschreibung der Elemente und ihrer Beziehungen in dem System zu geben, hier etwa der Beziehungen zwischen Fried- und Raubfischen in einem aquatischen Ökosystem oder zwischen Hasen und Luchsen in der kanadischen Tundra (Abb. 1B). Auf diesen Beispielen beruhen im wesentlichen die klassischen biologischen Räuber-Beute-Modelle.

Soll ein solches Modell für Prognosen herangezogen werden, muß es formalisiert und quantifiziert werden. Dies ist der entscheidende Schritt der Mathematisierung. In unserem Beispiel werden dazu zwei gekoppelte Differential- bzw. Differenzengleichungen erster Ordnung benötigt (Abb. 1C). Dieser Gleichungstyp ist charakteristisch für dynamische Systeme. Da das Gleichungssystem nicht bzw. nur näherungsweise mathematisch-analytisch behandelt werden kann, wird es als ablauffähiges Simulationsprogramm auf dem Computer implementiert (Abb. 1D).

Mit den gewünschten Parameterwerten kann das Simulationsprogramm gestartet werden. Schließlich werden die resultierenden Ergebnisdaten interpretiert (Abb. 1E). Das Ergebnis des Vergleichs der Daten mit empirischen Befunden kann - im negativen Fall - eine Modifikation, Erweiterung oder Neuentwicklung des Modells verlangen, oder - im positiven Fall - das Modell als Grundlage weiterer Untersuchungen bestätigen.

Die Modellentwicklung wird selten in einem einzigen Schritt erfolgen. Sie erfordert in der Regel mehrere Revisionsphasen. Dies wird die Modellvalidierung genannt. Kann ein validiertes Modell in eine operable Form (z.B. eben in ein Computerprogramm) gebracht werden, können Simulations-"Experimente" durchgeführt werden.

Modelle sind nicht beziehungslos, sondern sie sind Abbilder eines ausgewählten Realitätsbereiches. Ihre Verwendung im Unterricht ist nicht auf die Vermittlung von Erkenntnissen über die Modelle beschränkt, sondern auf den Realitätsbereich selbst gerichtet. Es ist deshalb eine dauernde Bewertung der Ergebnisse in Bezug auf den Realitätsbereich notwendig und damit ein Wechsel der Betrachtungsebene Modell und Realität, d.h. ein dauernder Wechsel von Abstraktion und Konkretion. Die Analyse der Daten bekommt dadurch ihr Ziel, sie kann zu neuen Hypothesen führen und effektiviert den Bearbeitungsprozeß.